custom search of this site
	N-clusters
	[chongo's home] [Astronomy] [Mathematics] [Prime Numbers] [Programming] [Technology] [contacting Landon]

General information about n_m-clusters

An n₂-cluster is n > 1 lattice points in R² such that no 3 are co-linear and no 4 are co-circular and all mutual distances between points are integers > 0.

In other words, a 2-dimension n₂-cluster is a collection of n lattice (grid points with integer (x,y) coordinates) on a flat plane such that no 3 lie on a straight line and no 4 lie on a circle and all of the distances between each pair of points are whole numbers > 0.

One need not be restricted to the R². We define n_m-clusters in R^m as follows:

• m and n are integers > 1
• n lattice points in R^m
• for all integer 0 < k < m, no k+2 points lie in k-dimensional plane (a k-dimensional affine subspace of R^m)
• for all integer 0 < l < m, no l+3 points lie on the surface of an l-dimensional sphere
• all mutual distances between the n lattice points are non-zero integers

n_m-cluster related terminology:

• prime n_m-cluster: an n_m-cluster where the greatest common divisor (gcd) of the mutual distances = 1
• primitive n_m-cluster: A prime n_m-cluster that has been rotated, reflected and translated into canonical form
  (Note to web page editor: define the canonical form here)

• equivalent n_m-cluster: two n_m-clusters are equivalent if and only if they can be made identical under the combined operations of rotation, reflection and translation
• nonequivalent n_m-cluster: two n_m-clusters that are not equivalent
  (all primitive n_m-clusters are both prime and nonequivalent)

• n-cluster: shorthand for n₂-cluster
• n(m)-cluster: alternate notation for n_m-cluster used in places where sub-scripting is not available or desirable

n₂-clusters

• n > 1 lattice points (points with integer (x,y) coordinates) in R²
• no 3 points lie on a straight line
• no 4 points lie on a circle
• all mutual distances between points are integers > 0

(0,0) (546,272) (132,720) (960,720) (546,-1120) (1155,-540)

The following are the smallest n₂-clusters:

(0,0) (1,0)

(0,0) (3,0) (0,4)

(0,0) (3,4) (3,-4) (6,0)

(0,0) (16,30) (-16,30) (0,-33) (56,0)

(0,0) (546,272) (132,720) (960,720) (546,-1120) (1155,-540)

A picture of the smallest 6₂-cluster is available.

UPDATE: 7₂-clusters DO exist!

Chuck Simmons and Landon Curt Noll discovered a number of 7₂-clusters on 2006-May-18 15:26:55 PDT:

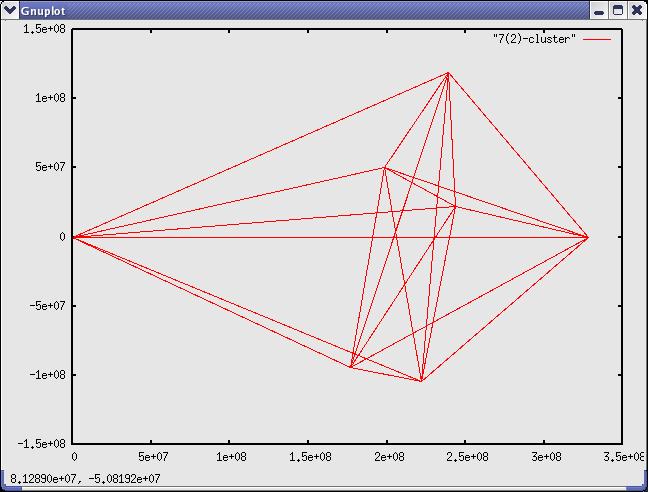
(0,0) (327990000,0) (238776720,118951040) (222246024,-103907232)
(243360000,21896875) (198368352,50379264) (176610000,-94192000)

NOTE: This 7₂-cluster is not be the smallest. The above mentioned 7₂-clusters simply prove that these strutures exist. The smallest 7₂-cluster is:

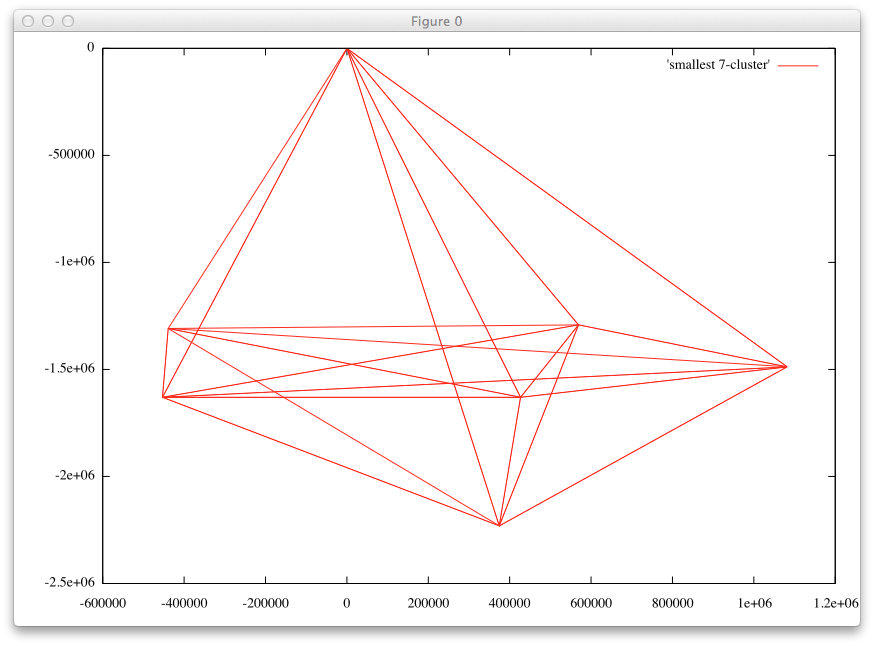
(0,0) (374400,-2230800) (1081600,-1488240) (-453024,-1630200)
(426725,-1630200) (569088,-1291680) (-439040,-1308720)

As recent as 2010-August-26, using an improved search algorithm, 25 nonequivalent (new) 7₂-clusters were discovered:

(68634995347500,46759948729375) (85941805950000,71210832840000) (68634995347500,4632341698125)
(130072970722500,48916330870000) (133822723450416,98216877284288) (137269990695000,0) (0,0)

(68634995347500,46759948729375) (51328184745000,71210832840000) (68634995347500,4632341698125)
(7197019972500,48916330870000) (3447267244584,98216877284288) (0,0) (137269990695000,0)

(8742402935396,-10550893265055) (12491072799192,-7329880708800) (1251972023796,-12174625385247)
(8742402935396,590045900847) (17484805870792,0) (0,0) (5153771043792,-23774836660350)

(8742402935396,-10550893265055) (4993733071600,-7329880708800) (16232833846996,-12174625385247)
(8742402935396,590045900847) (0,0) (17484805870792,0) (12331034827000,-23774836660350)

(57074946589137,-29602439091140) (68119373772450,-49995038226600) (57074946589137,6361294356684)
(108165052231587,-40677455540084) (96768547697250,-80181802070200) (114149893178274,0) (0,0)

(57074946589137,-29602439091140) (46030519405824,-49995038226600) (57074946589137,6361294356684)
(5984840946687,-40677455540084) (17381345481024,-80181802070200) (0,0) (114149893178274,0)

(127760562354100,174076664586825) (189715358500200,126876727286400) (18296188244100,177918702348075)
(127760562354100,14239567321200) (255521124708200,0) (0,0) (12519023151384,356682343821888)

(127760562354100,174076664586825) (65805766208000,126876727286400) (237224936464100,177918702348075)
(127760562354100,14239567321200) (0,0) (255521124708200,0) (243002101556816,356682343821888)

(1481541457500,-537780709375) (1665923415000,0) (832961707500,-1005271678125)
(832961707500,432023150000) (1550362069464,1036842072448) (0,0) (1523288063400,-2113353748800)

(184381957500,-537780709375) (0,0) (832961707500,-1005271678125)
(832961707500,432023150000) (115561345536,1036842072448) (1665923415000,0) (142635351600,-2113353748800)

(5272996965444,-1914030845545) (5929236112488,0) (2964618056244,-4039359357033)
(2964618056244,2019747908633) (6173748624888,3622814603200) (0,0) (6745851981888,-7326859050450)

(5272996965444,-1914030845545) (5929236112488,0) (2964618056244,-4039359357033)
(2964618056244,2019747908633) (6173748624888,3622814603200) (0,0) (6745851981888,-7326859050450)

(656239147044,-1914030845545) (0,0) (2964618056244,-4039359357033)
(2964618056244,2019747908633) (-244512512400,3622814603200) (5929236112488,0) (-816615869400,-7326859050450)

(1481541457500,-537780709375) (1665923415000,0) (832961707500,-1005271678125)
(832961707500,432023150000) (1550362069464,1036842072448) (0,0) (1523288063400,-2113353748800)

(184381957500,-537780709375) (0,0) (832961707500,-1005271678125)
(832961707500,432023150000) (115561345536,1036842072448) (1665923415000,0) (142635351600,-2113353748800)

(68634995347500,46759948729375) (85941805950000,71210832840000) (68634995347500,4632341698125)
(130072970722500,48916330870000) (133822723450416,98216877284288) (137269990695000,0) (0,0)

(68634995347500,46759948729375) (51328184745000,71210832840000) (68634995347500,4632341698125)
(7197019972500,48916330870000) (3447267244584,98216877284288) (0,0) (137269990695000,0)

(8742402935396,-10550893265055) (12491072799192,-7329880708800) (1251972023796,-12174625385247)
(8742402935396,590045900847) (17484805870792,0) (0,0) (5153771043792,-23774836660350)

(8742402935396,-10550893265055) (4993733071600,-7329880708800) (16232833846996,-12174625385247)
(8742402935396,590045900847) (0,0) (17484805870792,0) (12331034827000,-23774836660350)

(57074946589137,-29602439091140) (68119373772450,-49995038226600) (57074946589137,6361294356684)
(108165052231587,-40677455540084) (96768547697250,-80181802070200) (114149893178274,0) (0,0)

(57074946589137,-29602439091140) (46030519405824,-49995038226600) (57074946589137,6361294356684)
(5984840946687,-40677455540084) (17381345481024,-80181802070200) (0,0) (114149893178274,0)

(127760562354100,174076664586825) (189715358500200,126876727286400) (18296188244100,177918702348075)
(127760562354100,14239567321200) (255521124708200,0) (0,0) (12519023151384,356682343821888)

(127760562354100,174076664586825) (65805766208000,126876727286400) (237224936464100,177918702348075)
(127760562354100,14239567321200) (0,0) (255521124708200,0) (243002101556816,356682343821888)

(214219880550,6301947600) (224858052864,-26545742352) (175084785954,0)
(121350268260,-110224651680) (134680604580,-179574139440) (0,0) (345929626949,-494479514400)

(617451851250,-875785365000) (780757128000,-819794984400) (525254357862,-700339143816)
(804949411500,-154727118000) (1122338371500,0) (0,0) (3015706938447,99720035404)

(1009529065706589428,0) (1203398391990949336,45860386955466720) (0,0)
(676939921408158408,985583027337548640) (53761902907451508,-563219935220920560)
(1246841707833420832,1354229751267244425) (2606346791263681648,-1834662143896632960)

(220244176831120,0) (246555468595800,12985596405600) (165138740488800,35797817293056)
(187901542064600,73409269700325) (242381054588400,120746605948800) (95836927172560,134624270161920) (0,0)

(1541709237817840,0) (1725888280170600,90899174839200) (1155971183421600,250584721051392)
(1315310794452200,513864887902275) (1982197591480080,1057172048789376) (670858490207920,942369891133440) (0,0)

(0,0) (-1203015538725,-2544411343500) (10749021956400,0) (19954499237400,4909587883200)
(11374103163150,-17184050629200) (23379026610072,-4158083198304) (24966478323150,2041480914200)

(1163564931724079313,-269477403542383960) (834417531683024619,0) (1455548309962875744,134645123549696760)
(270089852186798469,-710440427520830440) (945507656505731319,829472932009543360) (0,0)
(540705461390553459,-3959673836535537120)

(2839035903168,420142221576) (2716494421875,0) (3488742000000,411865375000)
(678132000000,-760880250000) (1889735250000,-1984222012500) (3053812164000,-2179591564500) (0,0)

(888913935,1185218580) (732147500,1624350000) (750638434,291746112)
(0,0) (1899388750,0) (1508338125,-938521500) (3000817152,354263136)

(90559954461600,-56348416109440) (66832836431400,-65671968304800) (99758004738288,0)
(62274616513200,7351864449475) (0,0) (76736926721760,102315902295680) (219297144627600,85232898316800)

(645746712,1432660320) (1133937120,1511916160) (920228400,108638075)
(0,0) (1474118256,0) (1338199200,-832657280) (3240541200,1259481600)

(46093983313228774560,7133592655618738920) (51205858532566473645,14766053479192164552) (30836021244266471870,0)
(37713496340872872000,-14317464299263259160) (48652889618418976800,-16680990726315077760)
(23093827308239198310,-11696944424489686080) (0,0)

(204525733500,0) (181222195380,31071384160) (116714131380,-89881235840)
(64902832764,110138140448) (107446130880,167222282535) (0,0) (195966456000,492121242000)

(1537489668,2659073040) (720014022,3200062320) (0,0)
(3448272282,0) (-1907771943,1360265200) (8837240832,1733306400) (970646382,-5946302160)

(1861671240,2343685344) (1416176720,1989335040) (2776610200,1084764525)
(3581650800,1784265600) (2440245600,528982272) (3254535440,0) (0,0)

(13031698680,16405797408) (9913237040,13925345280) (19436271400,7593351675)
(17081719200,3702875904) (29290818960,15621770112) (22781748080,0) (0,0)

(18880367688,-8041182240) (19189941309,-15711063060) (20689633692,0)
(28850942484,-6681773280) (26355138250,5713113840) (37802741526,-10726662720) (0,0)

(5722762500,7204470000) (6540315210,9187326720) (6160119966,3068777712)
(8604820224,3361726368) (10778796875,2336565000) (8461703250,0) (0,0)

(5722762500,7204470000) (6540315210,9187326720)
(5123868750,2732730000) (8604820224,3361726368) (10778796875,2336565000) (8461703250,0) (0,0)

(154949507036870777,-230980631607757680) (69052004404618851,-181633390270652760) (91144391325948576,-327981711210799800)
(176997658235793101,0) (-102311826723971249,-274457955444334200) (0,0) (906675315979444011,209982703452642120)

(4959471309432841342089,0) (5145703589278133161956,-1817658122369063017680) (2728622318116179176640,819077651069860662480)
(3631649471438236223040,2723737103578677167280) (5383609759475803626444,3592702165069798173360) (0,0)
(50220507702021572864,1908048894599832784800)

(335600575349000,223959939060000) (460196641548696,345147481161522) (526540779804000,0)
(451186570951000,-159376248780000) (0,0) (877918993526536,263533660291902) (35997201279000,1367656824909375)

(220540073481,238652060192) (164939775000,277533828000) (270450480300,0)
(0,0) (-140026136250,336062727000) (299378956800,679511448000) (760141882500,493806456000)

(3749181249177,4057085023264) (2803976175000,4718075076000) (4597658165100,0)
(0,0) (-1487477641650,8113514409000) (5089442265600,11551694616000) (12922412002500,8394709752000)

(21945462903,10830898260) (21142072098,0) (37836432900,12972491280)
(0,0) (8666936388,38519717280) (54627962688,-22761651120) (60508055894,68284953360)

(122766861254427,47715055386336) (139881033166875,0) (0,0)
(100323715366875,205792236650000) (274032673366875,100613730150000) (-22482696967185,190441668427920)
(-38698090055625,-377699815350000)

(90026022240,262575898200) (0,0) (473881430880,419911601252)
(-110715848880,631802398500) (427936195995,0) (680445131520,779676713200) (1105723338720,460718057800)

Pictures and coordinates of twenty-five recently found 7-clusters

N-Cluster Search: Progress Update (as of 2010-Oct)

It should be noted that Tobias Kreisel and Sascha Kurz reported the discovery of two 7-element integral heptagons. While these 7-element integral heptagons are 7 points in R², no 3 co-linear and no 4 are co-circular and all mutual distances between points are integers > 0, their coordinates are not lattice points in R². Because some of their points are not lattice points in R² (i.e., some points do not have integer (x,y) coordinates) they are not 7₂-clusters:

There are Integral Heptagons, No Three Points on a Line, No Four on a Circle

Even so, this above work and results of Kruz and Kreisel is impressive and is worth reading.

n₃-clusters

• n lattice points (points with integer (x,y,z) coordinates) in R³
• no 3 points lie on a straight line
• no 4 points lie on a flat plane
• no 4 points lie on a circle

  NOTE: If no 4 points lie on a flat plane, then no 4 points can lie on a circle and therefore the above test may be skipped.

• no 5 points lie on the surface of a sphere
• all mutual distances between points are integers > 0.

(0,0,0) (54,28,12) (30,-20,60) (12,-56,-72) (-3,-76,-12) (-30,-84,12) (-72,0,96)

(0,0,0) (21,20,0) (-87,-4,-72) (108,24,-72) (126,-120,0) (-3,-172,96) (24,192,96)

The following are the smallest n₃-clusters:

(0,0,0) (1,0,0)

(0,0,0) (2,2,1) (2,2,-1)

(0,0,0) (2,2,1) (2,2,-1) (0,4,0)

(0,0,0) (6,6,3) (6,-6,3) (8,0,0) (8,0,6)

(0,0,0) (12,12,6) (-8,0,15) (-4,12,18) (20,0,15) (8,24,12)

(0,0,0) (54,28,12) (30,-20,60) (12,-56,-72) (-3,-76,-12) (-30,-84,12) (-72,0,96)

n₄-clusters

A n₄-cluster is:

• n lattice points (points with integer (x,y,z,w) coordinates) in R⁴
• no 3 points lie on a straight line
• no 4 points lie on a plane
• no 5 points lie on a hyper-plane (an R⁴ plane)
• no 4 points lie on a circle

  NOTE: If no 4 points lie on a flat plane, then no 4 points can lie on a circle and therefore the above test may be skipped.

• no 5 points lie on the surface of a sphere

  NOTE: If no 5 points lie on a hyper-plane (an R⁴ plane), then no 5 points lie on the surface of a sphere and therefore the above test may be skipped.

• no 6 points lie on the surface of a hyper-sphere (an R⁴ sphere)
• all mutual distances between points are integers > 0.

Randall and I (well Randall did all of the coding and I kibitzed and theorized on the side :-)) found these 7₄-clusters on 8 June 2001:

(0,0,0,0) (8,4,1,0) (0,8,-4,-8) (8,-4,5,-8) (-4,-4,11,4) (4,0,-6,-12) (12,8,-10,4)

(0,0,0,0) (8,8,4,0) (8,-8,4,0) (0,12,6,-4) (0,0,-9,12) (12,0,9,8) (8,4,10,12)

(0,0,0,0) (4,4,4,1) (4,-4,4,1) (-8,-4,4,10) (0,0,0,12) (0,12,-4,6) (0,12,12,6)

(0,0,0,0) (5,5,5,5) (8,-8,8,8) (-3,9,3,1) (5,1,11,-7) (0,-6,12,4) (0,-6,12,-12)

(0,0,0,0) (4,4,4,1) (-4,4,4,1) (-4,-8,4,10) (0,0,0,12) (12,0,-4,6) (12,0,12,6)

(0,0,0,0) (10,8,2,1) (10,-8,2,1) (0,0,0,12) (12,0,4,-6) (-6,-12,10,9) (12,0,-12,6)

and this 8₄-clusters on 10 June 2001:

(0,0,0,0) (8,8,8,8) (8,-10,4,-4) (0,-6,-12,4) (12,-3,-6,-6) (0,-9,-6,-18) (-12,-15,18,-6) (8,-25,-22,14)

The following are the smallest n₄-clusters:

(0,0,0,0) (1,0,0,0)

(0,0,0,0) (1,1,1,1) (1,1,1,-1)

(0,0,0,0) (1,1,1,1) (1,1,-1,1) (0,0,0,2)

(0,0,0,0) (4,3,0,0) (-4,3,0,0) (0,2,4,-4) (4,1,4,4)

(0,0,0,0) (4,2,2,1) (-4,2,2,1) (0,0,0,6) (0,6,2,3) (0,6,-6,3)

(0,0,0,0) (8,4,1,0) (0,8,-4,-8) (8,-4,5,-8) (-4,-4,11,4) (4,0,-6,-12) (12,8,-10,4)

(0,0,0,0) (8,8,8,8) (8,-10,4,-4) (0,-6,-12,4) (12,-3,-6,-6) (0,-9,-6,-18) (-12,-15,18,-6) (8,-25,-22,14)

n₅-clusters

A n₅-cluster is:

• n lattice points (points with integer (x,y,z,w,v) coordinates) in R⁵
• no 3 points lie on a straight line
• no 4 points lie on a plane
• no 5 points lie on a hyper-plane (an R⁴ plane)
• no 6 points lie on a 5-flat (an R⁵ plane)
• no 4 points lie on a circle

  NOTE: If no 4 points lie on a flat plane, then no 4 points can lie on a circle and therefore the above test may be skipped.

• no 5 points lie on the surface of a sphere

  NOTE: If no 5 points lie on a hyper-plane (an R⁴ plane), then no 5 points lie on the surface of a sphere and therefore the above test may be skipped.

• no 6 points lie on the surface of a hyper-sphere (an R⁴ sphere)

  NOTE: If no 6 points lie on a 5-flat (an R⁵ plane), then no 6 points lie on the surface of a hyper-sphere and therefore the above test may be skipped.

• no 7 points lie on the surface of a 5-sphere (an R⁵ sphere)
• all mutual distances between points are integers > 0.

Randall and I (as before) co-discovered these 8₅-clusters:

(0,0,0,0,0) (11,10,2,0,0) (13,6,2,0,4) (0,8,8,8,8) (4,12,8,4,4) (11,10,2,0,8) (13,6,2,8,4) (8,6,6,2,2)

(0,0,0,0,0) (6,6,6,6,0) (4,4,8,8,3) (10,2,10,6,4) (8,4,12,4,4) (4,8,8,12,1) (4,4,16,8,3) (8,4,12,8,1)

(0,0,0,0,0) (5,4,2,2,0) (0,8,4,8,0) (0,10,2,6,2) (5,14,0,8,2) (1,6,12,12,6) (8,10,2,14,6) (1,8,2,6,4)

(0,0,0,0,0) (5,4,2,2,0) (0,8,4,8,0) (0,10,2,6,2) (5,10,8,8,6) (1,12,6,6,12) (8,10,2,14,6) (1,6,4,8,2)

(0,0,0,0,0) (11,10,2,0,0) (13,6,2,0,4) (0,8,8,8,8) (4,12,8,4,4) (11,10,2,0,8) (9,14,2,8,4) (8,6,6,2,2)

(0,0,0,0,0) (8,4,4,4,3) (8,0,0,8,4) (6,10,2,6,7) (16,0,0,0,0) (10,2,10,6,7) (8,4,16,4,3) (8,4,4,8,6)

(0,0,0,0,0) (6,6,6,6,0) (0,12,4,8,1) (10,10,2,6,4) (8,12,4,8,1) (8,12,0,12,3) (4,16,4,8,3) (4,8,4,8,3)

(0,0,0,0,0) (6,6,6,6,0) (4,4,8,8,3) (10,2,10,6,4) (4,8,8,12,1) (8,0,12,12,3) (4,4,16,8,3) (8,4,12,8,1)

(0,0,0,0,0) (12,8,4,4,4) (12,5,10,2,4) (12,10,4,0,8) (12,6,12,0,0) (16,7,2,6,4) (4,13,10,10,12) (8,7,2,6,4)

(0,0,0,0,0) (8,0,0,0,0) (4,12,4,4,8) (8,10,10,4,3) (4,10,2,0,13) (12,8,4,0,10) (4,4,12,12,16) (4,8,4,8,6)

as well as these 9₅-clusters on 26 July 2001:

(0,0,0,0,0) (2,0,-2,4,-5) (4,-4,-4,4,0) (4,4,-8,0,-2) (-4,-4,0,8,-2) (-8,8,-4,4,6)
(-4,4,-4,12,8) (-8,-8,-8,0,-8) (0,2,-4,6,-5)

(0,0,0,0,0) (0,8,0,0,0) (4,4,0,4,-4) (0,6,-3,6,0) (0,6,5,-2,-4) (8,4,-10,0,4) (8,4,-6,-8,-4)
(0,-4,-10,-8,-4) (-8,4,-6,-8,-4)

The following are the smallest n₅-clusters:

(0,0,0,0,0) (1,0,0,0,0)

(0,0,0,0,0) (1,1,1,1,0) (0,0,0,2,0)

(0,0,0,0,0) (2,2,1,0,0) (0,0,1,2,2) (2,2,0,2,2)

(0,0,0,0,0) (2,2,1,0,0) (0,0,1,2,2) (2,2,0,2,2) (0,0,0,0,4)

(0,0,0,0,0) (2,2,1,0,0) (0,0,1,2,2) (2,2,0,2,2) (0,0,0,0,4) (0,4,1,2,2)

(0,0,0,0,0) (5,4,2,2,0) (5,2,0,4,2) (0,4,4,4,4) (0,0,0,8,0) (5,6,0,4,2) (6,4,4,4,4)

(0,0,0,0,0) (11,10,2,0,0) (13,6,2,0,4) (0,8,8,8,8) (4,12,8,4,4) (11,10,2,0,8) (13,6,2,8,4) (8,6,6,2,2)

(0,0,0,0,0) (2,0,-2,4,-5) (4,-4,-4,4,0) (4,4,-8,0,-2) (-4,-4,0,8,-2) (-8,8,-4,4,6) (-4,4,-4,12,8) (-8,-8,-8,0,-8)
(0,2,-4,6,-5)

open n_m-cluster questions, conjectures & observations

n_m-cluster conjectures:

• Erdös/Noll infinite-or-bust n_m-cluster conjecture:
  For any m > 1, n > 2, there exists either 0 or an infinite number of primitive n_m-clusters.
• Noll infinite n_m-cluster conjecture:
  For any m > 1, n > 2, there exists an infinite number of primitive n_m-clusters.
• Noll/Rathbun computation observation:
  For any m > 1:
  • One will be able to find many (m+3)_m-clusters;
  • With bit more effort, one will also find some: (m+4)_m-clusters;
  • However, finding an (m+5)_m-cluster will be a significant computational challenge.

Open questions about n_m-clusters:

• No 8₂-cluster has ever been found. Do 8₂-clusters exist?
• No 8₃-cluster has ever been found. Do 8₃-clusters exist?
• No 9₄-cluster has ever been found. Do 9₄-clusters exist?
• No 10₅-cluster has ever been found. Do 10₅-clusters exist?

For more information see:

• Unsolved Problems in Number Theory, problem D20.
• '' n-clusters for 1 < n < 7,'' Landon Curt Noll and David I Bell; Mathematics of Computation, Vol 53, Number 187, July 1989, Pages 439-444.